Online interaktivni priručnik za kompjuterski adaptivno testiranje, 11/98 (http://EdRes.org/scripts/cat)

Lawrence M. Rudner
ERIC Clearinghouse on Assessment and Evaluation

Dobrodošli na naš online priručnik za kompjuterski adaptivno (prilagodljivo) testiranje (CAT, " computer adaptive testing"). Ovdje ćete imati priliku naučiti logiku CAT-a i vidjeti izračune koji se izvode u pozadini. Možete se igrati sa stvarnim CAT-om. Mi pružamo pitanja i točne odgovore. Možete isprobati različite scenarije i vidjeti što se događa. Možete se pretvarati da ste visoko sposoban, prosječan ili nisko sposoban kandidat. Možete namjerno pogriješiti na lakim pitanjima/česticama. Možete ispravno odgovoriti na pitanja koja bi trebala biti vrlo teška za vas.

Ovaj priručnik pretpostavlja određeno predznanje iz statistike ili iz mjerenja. Ipak, nadam se da će i početnik moći pratiti sadržaj.

Sadržaj (linkovi):

Kako radi demo

Predložene aktivnosti

Skup čestica

Počnimo (Ovdje počinje CAT)

Pozadina

Što i zašto o CAT-u

Neki termini

Ponešto o teoriji odgovora na pitanja (item response teoriji , IRT)

Logika CAT-a

Pouzdanost i standardna pogreška

Mogućnosti i ograničenja CAT-a

Ključna tehnička i proceduralna pitanja

Interaktivni IRT mini-priručnik (Generirajte grafove funkcija odgovora na pitanja (item response functions))

Pretraga ERIC baze podataka na temu CAT metodologije

Dodatni izvori na Internetu

Reference i daljnje čitanje

Zahvale

Predložene aktivnosti

Ovaj sustav vam dopušta da se igrate sa različitim scenarijima. Možete mijenjati

· svoj pravi rezultat. Ovo je stvarna sposobnost koju test nastoji procijeniti. Ovaj priručnik koristi tu vrijednost kako bi pobliže objasnio što se događa u pozadini. Ta vrijednost se ne koristi u izboru čestica/pitanja ni u izračunavanju standardnih pogrešaka.

· mjeru u kojoj odgovarate na očekivan način. Program će pružiti vjerojatnost ispravnog odgovora na osnovu (procjene) vašeg pravog rezultata. Možete pogrešno odgovoriti na laka pitanja i točno na teška ukoliko to želite. Možete izabrati učestalost neočekivanih odgovora.

· broj pitanja na koja odgovarate. To odražava različita pravila za prestanak.

· skalu koja se koristi za definiranje sposobnosti.

Tijekom postupka testiranja, sustav će vam pokazati:

· informacijske funkcije za 5 čestica za koje računalo očekuje da će vam pružiti najviše informacija o vašoj razini sposobnosti. S obzirom da se čestice biraju na osnovu računalne procjene vaše sposobnosti, izabrane čestice možda neće biti najbolje s obzirom na vašu pravu/istinsku sposobnost.

· funkcija odgovora na česticu ("Item Response Function") za izabranu česticu.

· Standardnu pogrešku trenutne procjene vaše sposobnosti.

Kada pritisnete "Done", sustav će vam pokazati tijek vašeg testiranja, uključujući i težine pitanja (čestica), vjerojatnosti ispravnog odgovora, da li ste odgovarali ispravno, procjene sposobnosti i standardne pogreške.

Kada prvi put budete koristili sustav za pristupanje CAT testiranju, predlažem vam da izaberete pravi rezultat koji je malo iznad prosjeka, odgovorite na pitanja onako kako program to sugerira, te odgovorite na otprilike 10 pitanja. Ova skupina pitanja je optimalna za pristupnike sa blago iznadprosječnim sposobnostima. Ako u potpunosti odgovarate onako kako je predviđeno IRT modelom, procjena sposobnosti će ubrzo konvergirati ka danom pravom rezultatu. Prilikom tog prvog isprobavanja, trebali biste primijetiti da:

· Program počinje sa procjenom sposobnosti na pedesetom centilu. U nedostatku dugih informacija, ovo je najrazumnija procjena.

· Nakon ispravnih odgovora slijede teža pitanja.

· Nakon pogrešnih odgovora slijede lakša pitanja.

· Nakon samo nekoliko pitanja, procjena sposobnosti je blizu vaše stvarne sposobnosti. Procjena sposobnosti se poboljšava povećanjem broja pitanja, naravno pod pretpostavkom da ste dosljedni u svom odgovaranju.

· Nakon samo nekoliko pitanja njihova težina je blizu vaše prave sposobnosti i vjerojatnosti ispravnog odgovora su blizu 0,50.

· Standardna pogreška se poboljšava povećanjem broja čestica.

Jednom kad ste upoznati sa programom, pokušajte pristupati testu pod drugim scenarijima:

· Isprobajte različite prave rezultate. Primijetite na koliko pitanja trebate odgovoriti da bi dobili prihvatljivu procjenu sposobnosti.

· Isprobajte dati nekoliko neočekivanih odgovora. Točno odgovorite na jako teško pitanje (tj., odgovorite točno kada je vjerojatnost točnog odgovora manja od 0,50), poput sretnog pogotka; ili na laku česticu pogrešno odgovorite, kao što bi bio slučaj kod pogreške zbog nepažnje. Primijetite da se procjena sposobnosti počinje odvajati od vašeg pravog rezultata, ali onda naglo počinje ponovno konvergirati Također možete eksperimentirati sa neočekivanim odgovorima na početku vs u sredini vs nakon 15 pitanja.

· Isprobajte davati mnoštvo neočekivanih odgovora. Primijetite da se procjena sposobnosti počinje odjeljivati od vašeg pravog rezultata, ali naposljetku ipak može konvergirati (pod pretpostavkom da ste opet počeli odgovarati onako kako se očekuje).

· Izaberite različit prag za točno odgovaranje. Npr., umjesto ispravnog odgovaranja kada je vjerojatnost točnog odgovora veća od 0,50, odgovorite ispravno čim je vjerojatnost ispravnog odgovora veća od 0,40 ili 0,60. Primijetite kako će program podcijeniti ili precijeniti vaš pravi rezultat.

Jeste li spremni da isprobate pravi kompjuterski adaptivan test? Prvo ćete biti pitani da izaberete pravi rezultat (true score) i skalu pravog rezultata (z, SAT ili centile; možete promijeniti skalu kad zaželite). CAT će zatim krenuti sa prvim pitanjem. Kako bi vam pomogli u shvaćanju onoga što se odvija u pozadini, biti će prikazani grafovi informacijskih funkcija, funkcija odgovora na pitanje za izabranu česticu, te standardna pogreška. Ako vam bilo koji od grafova nije jasan, pritisnite gumb "Explain" i pojavit će se detaljne informacije. Informacije prikazane gumbom "Explain" se mijenjaju kako CAT napreduje, pa možete pritisnuti gumb više puta. Nakon što ste odgovorili na otprilike 10 čestica, možete pritisnuti gumb "Done". Biti će prikazani vaši odgovori. Ako odgovorite na više od 5 pitanja, biti će prikazani i pregledni grafovi. Zabavite se. Ako imate prijedloge za aktivnosti ili poboljšanja, javite (Lawrence M. Rudner, rudner@ericae.net).

Set pitanja

Pitanja prikazana u ovom priručniku su od strane National Assessment of Educational Progress javno objavljena pitanja iz testa matematike za osmi razred. Naš skup pitanja sadrži 64 pitanja tipa višestrukog izbora. Slike su nanovo iscrtane kako bi se poboljšala kvaliteta (Javno objavljene čestice su dostupne na NAEP-ovim stranicama u Adobe formatu).

Skup pitanja je premalen za pravi CAT. Dva ili tri puta više čestica bi omogućilo programu da izabere kvalitetnije čestice na svakoj razini procjene sposobnosti. Kako bismo kompenzirali manjak čestica, povećali smo njihovu statističku kvalitetu dodavanjem 0,4 parametru razlikovanja čestica. Sa diskriminativnijim česticama, željene razine preciznosti u procjenama sposobnosti mogu se postići brže, tj., uz primjenu manjeg broja ispitnih pitanja. Stoga, ovo omogućava CAT programu da brže konvergira.

Testne informacije za ovu skupinu čestica prikazane su na slijedećem grafu:

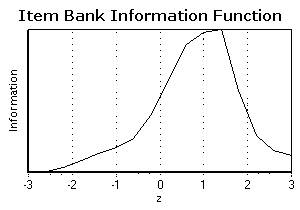
Primijetite da je ova skupina čestica najbolja za ispitanike čija je sposobnost između z- vrijednosti 0 i 2 (od 50og do 98og centila). Demo će naglo konvergirati za ispitanike čija je prava/stvarna sposobnost unutar tog raspona. Ovaj CAT nije dobro prilagođen za ispitanike na nižem kraju spektra sposobnosti.

Što i zašto o kompjuterski adaptivnom testiranju

Kada se pristupniku da test preko računala, računalo može obnoviti procjenu pristupnikove sposobnosti nakon svake čestice, te se zatim ta procjena sposobnosti može iskoristiti pri izboru slijedećih pitanja. Sa odgovarajućim skupom pitanja i visokim varijabilitetom sposobnosti pristupnika, CAT može biti mnogo efikasniji od tradicionalnih testova tipa papir – olovka.

Testovi tipa papir – olovka obično su testovi "fiksnih pitanja" u kojima ispitanici odgovaraju na ista pitanja unutar dane knjižice. S obzirom da svi odgovaraju na sva pitanja, svim pristupnicima su dana pitanja koja su ili prelagana ili preteška za njih. Ta laka i teška pitanja su poput nadodavanja konstante na nečiji rezultat. Ona pružaju relativno malo informacija o ispitanikovoj razini sposobnosti. Posljedično, veliki broj pitanja i ispitanika je potreban za dobivanje umjerene razine preciznosti. Sa kompjuterski adaptivnim testovima, ispitanikova razina sposobnosti u odnosu na grupnu normu može se iterativno (repetitivno, ponovno) procijeniti tijekom procesa testiranja i pitanja se mogu birati na osnovu procjene trenutne sposobnosti. Ispitanicima se mogu dati pitanja koja maksimaliziraju informaciju (unutar granica) o njihovim razinama sposobnosti na osnovu odgovora na pitanje. Stoga, ispitanici će dobiti malo pitanja koja su jako laka ili jako teška za njih. Ova prilagođena selekcija čestica može rezultirati manjim standardnim pogreškama i većom preciznošću sa samo nekoliko dobro izabranih čestica.

Neki pojmovi

Kako bih objasnio logiku kompjuterski adaptivnog testiranja , trebam prvo definirati neke termine i koncepte mjerenja.

Neki termini:

Pravi rezultat – Rezultat kojega će ispitanik dobiti nakon savršeno pouzdanog testa. S obzirom da svi testovi sadrže pogrešku, pravi rezultati su teoretski koncept; u stvarnom programu testiranja nikada nećemo znati pojedinčev pravi rezultat. Međutim, mi možemo izračunati procjenu ispitanikova pravog rezultata i možemo procijeniti količinu pogreške u toj procjeni. Prava sposobnost se označava sa theta (); pravi rezultat ispitanika j se označava theta-j ().

Procjena sposobnosti – Rezultat kojega možete dobiti na osnovu rješavanja stvarnog testa. Također se naziva procjenom pravog rezultata. Procjena prave sposobnosti se označava sa theta-hat (theta s kapom) ().

Standardna pogreška – U svakoj situaciji testiranja postoje višestruki izvori pogreške. Dio te pogreške može biti posljedica varijacija u manifestnom ponašanju ispitanika (tj. kad imaju loš dan). Najveći pojedinačni izvor pogreške je obično posljedica izbora sadržaja testa ("sampling of test content"). Standardna pogreška je procjena standardne devijacije procjena sposobnosti koje se mogu očekivati za danog ispitanika, kada bi taj ispitanik mnogo puta polagao ekvivalentne oblike testa bez učenja ili poduka između tih primjena.

Neki koncepti:

Vjerojatnost ispravnog odgovora – Obično se misli na pojedinca koji ili točno ili krivo odgovori. Pretpostavimo da imamo mnoštvo ljudi sa nekim uobičajenim pravim rezultatom (theta-j: ), te da oni odgovaraju na pitanje. Neki od tih ljudi će na pitanje odgovoriti točno, drugi će pogrešno. Postotak onih koji su točno odgovorili na pitanje biti će vjerojatnost ispravnog odgovora uz danu specifičnu vrijednost za theta. Za bilo koju danu česticu (pitanje), očekivali bismo da će vjerojatnost točnog odgovora biti niska (blizu pogađanja) za ispitanike niskih sposobnosti, te visoka (blizu sigurnosti) za ispitanike visokih sposobnosti.

Funkcija odgovora na česticu (item response function) {povratna funkcija zadatka*}– Kada imamo vjerojatnosti točnih odgovora za cijeli raspon sposobnosti, (tj. Theta vrijednosti), tada imamo funkciju koja stavlja u odnos sposobnost sa vjerojatnošću ispravnog odgovora. Također se naziva krivuljom karakterističnom za česticu ("item characteristic curve" {karakteristika zadatka*}). Jedna takva funkcija je definirana u slijedećem odlomku.

Teorija odgovora na čestice (IRT - "item response theory") {teorija povratne informacije zadatka*}– Teoretski okvir koji daje funkcije odgovora na čestice{povratne funkcije zadataka*} i ekstenzije tih funkcija. Rasch model, logistički model tri parametra i Birnbaum model dva parametra su IRT modeli. Ovi IRT modeli stavljaju u odnos vjerojatnost ispravnog odgovaranja na čestice sa karakteristikama čestica i ispitanikovom pravom sposobnošću {povezuju vjerojatnost točnog odgovora sa karakteristikama zadatka i mogućnostima ispitanika*}.

Ponešto o teoriji odgovora na čestice

IRT je statistički okvir u kojem se ispitanici mogu opisati setom jednog ili više rezultata sposobnosti koji su prediktivni kroz matematičke modele, povezivanje stvarnog izvođenja na testnim česticama, statističke parametre čestice i ispitanikove sposobnosti {Teorija povratne informacije zadatka (TPIZ) je statistički model u kojem se ispitanik može predstaviti skupom jedne ili više mogućnosti točnog odgovora koji povezuje stvarne performanse na ispitu, statistiku zadataka i mogućnosti ispitanika (znanje ispitanika)*}. Pogledajte van der Linden i Hambleton (1997), Hambleton, Swaminathan, i Rogers (1991) i Hambleton i Jones (1993) za daljnja objašnjenja IRT-a.

Ovaj priručnik koristi široko prihvaćen IRT model triju parametara kojega je prvi opisao Birnbaum (1968). Pod IRT modelom 3 parametra, vjerojatnost ispravnog odgovora na danu česticu je funkcija ispitanikove prave sposobnosti i triju parametara čestice.

1. a_i, ili parametar diskriminativnosti čestice,
2. b_i, ili parametar težine čestice, i
3. c_i, ili parametar pogađanja.

Svaka čestica i ima različit set tih triju parametara. Ti parametri se obično izračunavaju na osnovu ranije primjene čestice (i cijelog testa).

Model kaže da je vjerojatnost ispravnog odgovora na česticu i za ispitanika j funkcija triju parametara čestice i prave sposobnosti ispitanika j.

P(u_i=1 | , a_i, b_i, c_i) = c_i + (1 - c_i) / [1 + exp(-1.7 a_i ( - b_i)]

Ova funkcija je dolje iscrtana sa a_i = 2.0, b_i = 0.0, c_i = .25 i koja varira od -3.0 do 3.0.

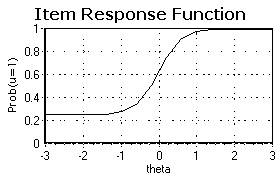
Horizontalna os je skala sposobnosti koja varira od vrlo niske (-3.0) do vrlo visoke (+3.0). Kada sposobnost prati normalnu krivulju, 68% ispitanika će imati sposobnost između -1 i +1; 95% će biti između -2.0 i +2.0. Vertikalna os je vjerojatnost ispravnog odgovaranja na tu česticu (definiranu sa njena tri parametra) uz = .

Donja asimptota je na c_i=.25. To je vjerojatnost ispravnog odgovora za ispitanike sa vrlo malom sposobnošću (npr., = -2.0 ili -2.6). Krivulja ima gornju asimptotu na 1.0; visoko sposobni ispitanici će vrlo vjerojatno odgovoriti ispravno.

Parametar b_i definira lokaciju krivuljine točke infleksije uzduž theta skale. Niže vrijednosti b_i će pomaknuti krivulju nalijevo, a više na desno. Parametar b_i ne utječe na oblik krivulje.

Parametar a_i definira nagib krivulje na njenoj točci infleksije. Krivulja bi bila ravnija sa nižom vrijednošću a_i, a strmija sa višom vrijednošću. Primijetite da kad je krivulja strma postoji velika razlika između vjerojatnosti točnog odgovora za a) ispitanike čija je sposobnost malo ispod (lijevo) točke infleksije i b) ispitanika čija je sposobnost malo iznad točke infleksije. Stoga a_i označava koliko dobro čestica može razlikovati između ispitanika sa neznatno različitom sposobnošću (unutar uskog djelotvornog raspona).

Jedna od pozitivnih osobina IRT-a je da se ne moraju raditi distribucijske pretpostavke o sposobnostima i skaliranje ("scaling " – razmjeravanje, dimenzioniranje) sposobnosti je arbitrarno. Uobičajeno je i praktično postaviti rezultate sposobnosti na skalu sa aritmetičkom sredinom 0 i standardnom devijacijom 1. Kada se napravi takvo skaliranje, uobičajeno je naći rezultate sposobnosti uglavnom između -3.0 i +3.0, ili drugim riječima, neovisno o distribuciji rezultata sposobnosti, uobičajeno je naći približno sve rezultate unutar tri standardne devijacije od srednjeg rezultata sposobnosti.

Ako je IRT za vas novost, potičem vas da se igrate sa mijenjanjem parametara čestice za ovu funkciju na http://128.8.182.4/scripts/cat/genicc.asp.

Logika kompjuterski adaptivnog testiranja

Kompjuterski adaptivno testiranje može početi kada postoji banka čestica sa dostupnim IRT statisticima za svaku česticu, kada je odabrana procedura za dobivanje procjena sposobnosti na temelju izvedbe ispitanika na česticama, te kada je odabran algoritam za sekvencioniranje skupa testnih pitanja (čestica) koje će se dati kandidatima. {Računalno-adaptivni testovi mogu početi ispitivanje tek kada je popunjen skup zadataka, kad za svaki zadatak postoji napravljena statistika, kada je izabrana procedura za dobivanje procjene mogućnosti ispitanika na temelju rješavanja zadataka, te kad postoji algoritam za izbor skupa zadataka koji će se postaviti ispitaniku.*}

CAT algoritam je obično iterativan proces (algoritam koji uključuje ponavljanje) sa slijedećim koracima:

1. Sve čestice koje još nisu bile administrirane (dane ispitaniku, primijenjene) se procjenjuju da bi se odredilo koju će biti najbolje primijeniti kao slijedeću na osnovu trenutne procjene razine sposobnosti.

2. "Najbolja" slijedeća čestica se primjenjuje i ispitanik odgovara.

3. Nova procjena sposobnosti se računa na osnovu odgovora na sve dotad primijenjene čestice.

4. Koraci 1 do 3 se ponavljaju dok se ne zadovolji kriterij prekida.

Više različitih metoda može se koristiti u izračunu statističkih parametara potrebnih u svakom od tih triju koraka. Hambleton, Swaminathan i Rogers (1991); Lord (1980); Wainer, Dorans, Flaughter, Green, Mislevey, Steinberg, Thissen (1990); i drugi pokazali su kako se to može postići korištenjem "Item Response" teorije.

Tretirajući parametre čestica kao dane (određene, poznate), procjena sposobnosti je vrijednost theta koja najbolje pristaje u model. Kada se ispitaniku da dovoljan broj pitanja, početna procjena sposobnosti ne bi trebala imati velik utjecaj na konačnu procjenu sposobnosti. Proces prilagodbe će brzo rezultirati primjenom razumno odabranih pitanja. Kriterij prekida može biti vrijeme, broj administriranih pitanja, veličina promjene u procjeni sposobnosti, pokrivenost sadržaja, indikator preciznosti kao što je standardna pogreška, ili kombinacija faktora.

Korak 1 se odnosi na izbor "najboljeg" slijedećeg pitanja. Malo informacija o ispitanikovoj razini sposobnosti se dobije kada ispitanik odgovori na pitanje koje je prelagano ili preteško. Prije ćemo htjeti dati pitanje čija je težina bliže ispitanikovoj sposobnosti. Nadalje, želimo dati pitanje koje dobro diskriminira između različitih ispitanika čije su razine sposobnosti blizu razine odabranog pitanja.

Koristeći "item response" teoriju možemo kvantificirati količinu informacija koju pruža čestica na određenoj (danoj) razini sposobnosti. Pod pristupom maksimuma informacija, pristupom korištenim u ovom priručniku, "najbolja" slijedeća čestica je ona koja pruža najviše informacija (u praksi ograničenja su inkorporirana u selekcijski proces). Sa IRT-om, maksimum informacija može se kvantificirati kao standardizirani nagib od P_i() za (theta-hat, procjena sposobnosti). Drugim riječima

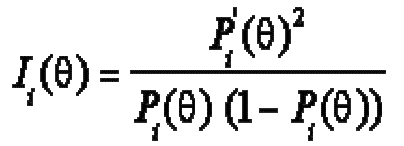
gdje je P_i() vjerojatnost ispravnog odgovora na česticu i, P^'_i() je prva derivacija ("first derivative") od P_i(), a I_i()je informacijska funkcija za česticu i.

Stoga, za korak 1, I_i() za svaku česticu može se procijeniti korištenjem trenutne procjene sposobnosti. Iako je maksimaliziranje informacija možda najbolji poznati pristup izboru čestica, Kingsbury i Zara (1989) opisuju nekoliko različitih procedura izbora čestica.

U koraku 3 izračunava se nova procjena sposobnosti. Pristup korišten u ovom priručniku je modifikacija Newton-Raphson iterativne metode za rješavanje jednadžbi, opisan u Lord-u (1980, p 181). Potraga ("examination") počinje početnom procjenom _S –a, izračunava vjerojatnost ispravnog odgovora za svaku česticu koristeći _S, te zatim prilagođava procjenu sposobnosti kako bi dobio bolje slaganje vjerojatnosti i opaženog vektora odgovora. Proces se ponavlja sve dok prilagodba ne postane ekstremno mala.

Stoga:

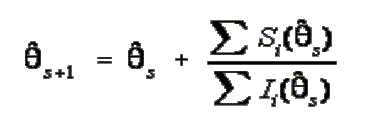
gdje

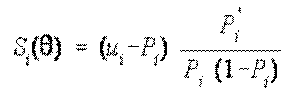
Desna strana gornje jednadžbe je prilagodba. _S+1 označava prilagođenu procjenu sposobnosti. Nazivnik prilagodbe je suma informacijskih funkcija čestice procijenjenih za _S. Kada je _S najvjerojatnija procjena ispitanikove sposobnosti, suma informacijskih funkcija čestice je informacijska funkcija testa, I_rr.

Standardna pogreška vezana uz procjenu sposobnosti se izračunava tako da se prvo odredi količina informacija koju set čestica dan kandidatu pruža na kandidatovoj razini sposobnosti – to se lako dobije sumiranjem vrijednosti informacijskih funkcija čestica na kandidatovoj razini sposobnosti kako bi se dobila informativnost testu. Drugo, informativnost testa ("the test information") se uvrsti u donju formulu kako bi se dobila standardna pogreška:

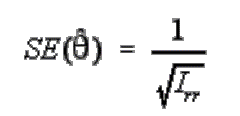
Dakle, standardna pogreška za pojedince se može dobiti kao nusprodukt izračunavanja procjene ispitanikove sposobnosti.

Pouzdanost i standardna pogreška

U klasičnom mjerenju, standardna pogreška mjerenja je ključni koncept i koristi se za opis razine preciznosti procjene prave sposobnosti. Sa pouzdanošću testa od 0.90, standardna pogreška mjerenja tog testa je 0,33 standardne devijacije ispitanikovih rezultata na testu. U mjerenju temeljenom na "item response" teoriji, te kada su rezultati sposobnosti izraženi na skali sa aritmetičkom sredinom 0 i standardnom devijacijom 1 (što je uobičajeno), ta razina pouzdanosti korespondira standardnoj pogrešci od otprilike 0.33 i informativnosti testa od otprilike 10. Stoga, u praksi je uobičajeno dizajnirati CAT-ove tako da su standardne pogreške otprilike 0,33 ili manje (ili korespondentno, informativnost testa nadilazi 10 – prisjetite se da ako je informativnost testa 10, odgovarajuća standardna pogreška je 0,33). [Ovom odlomku je pridonio Ron Hambleton, University of Massachusetts].

Potencijal kompjuterski adaptivnih testova

Općenito, kompjuterizirano testiranje uvelike povećava fleksibilnost upotrebe testova. Njihov potencijal je često opisivan (npr.: Urry, 1977; Grist, Rudner, i Wise, 1989; Kreitzberg, Stocking, i Swanson, 1978; Olsen, Maynes, Slawson i Ho, 1989; Weiss i Kingsbury, 1984; Green, 1983). Neke od prednosti su:

• Testovi se daju "na zahtjev" i rezultati su odmah dostupni.
• Nisu potrebni papiri za odgovore niti trenirani administratori testova. Razlike među administratorima testova su eliminirane kao faktor u pogrešci mjerenja.
• Testovi su prilagođeni pojedincu pa on ne mora čekati da drugi završe kako bi mogao prijeći na slijedeći dio testa. Ispitanici sami određuju ritam ispunjavanja testa što im pruža dodatno vrijeme ako ga trebaju, te se tako potencijalno reducira jedan izvor ispitne anksioznosti.
• Sigurnost testova se može povećati jer se ne rade papirnate kopije testova i njihovih brošura. {slobodno prevedeno: "because hard copy test booklets are never compromised"}.
• Kompjuterizirano testiranje pruža brojne opcije oblikovanja formata i vremena primjene {"timing and formatting"). Stoga ima potencijal da se prilagodi širem rasponu različitih tipova čestica.
• Značajno manje vremena je potrebno za primjenu CAT-ova negoli testova sa fiksnim česticama s obzirom da je potrebno manje čestica za postizanje prihvatljive točnosti. CAT-ovi mogu reducirati trajanje testiranja za više od 50% zadržavajući istu razinu pouzdanosti. Kraće trajanje testiranja također reducira umor, faktor koji može značajno utjecati na ispitanikove rezultate na testu.
• CAT-ovi pružaju precizne rezultate za cijeli raspon sposobnosti dok su tradicionalni testovi obično najprecizniji za prosječne ispitanike.

Ograničenja

Unatoč gore navedenim prednostima, kompjuterski adaptivni testovi imaju brojna ograničenja, te postavljaju nekoliko tehničkih i proceduralnih problema:

• CAT-ovi nisu primjenjivi za sve ispitanike ni sve sposobnosti. Većina CAT-ova je temeljena na "item-response" teoretskom modelu, a ta teorija nije primjenjiva na sve vještine i vrste čestica.
• Hardverska ograničenja mogu ograničiti tipove čestica koje se mogu primijeniti računalom. Na primjer, može biti teško prezentirati čestice koje uključuju detaljni umjetnički rad i grafove ili opsežne tekstove.
• CAT-ovi zahtijevaju pažljivu kalibraciju čestica. Parametri čestice korišteni pri testiranju olovkom i papirom možda se ne održe na kompjuterski prilagodljivom testu.
• CAT-ovi su smisleni samo ako ustanova ima dovoljno računala za velik broj ispitanika i ako su ispitanici barem djelomično kompjuterski pismeni. To može biti veliko ograničenje.
• Procedure primjene testova su različite. To može stvarati problem kod nekih ispitanika.
• S obzirom da svaki ispitanik dobiva različit skup pitanja, može biti razlika u shvaćanju {"perceived inequities" doslovni prijevod: opaženih nejednakosti}.
• Ispitanicima obično nije dozvoljeno da se vrate unatrag i promijene odgovore. Lukav ispitanik bi mogao namjerno pogriješiti na početnim pitanjima. CAT program bi onda pretpostavio nisku razinu sposobnosti i izabrao seriju lakih pitanja. Ispitanik bi se zatim mogao vratiti unatrag i promijeniti odgovore u točne. Rezultat bi mogao biti 100% točnih odgovora što bi rezultiralo procjenom ispitanikove sposobnosti kao najviše moguće.

Ključna tehnička i proceduralna pitanja

U literaturi postoji poprilična količina uputa o tehničkim, proceduralnim i pitanjima nepristranosti (equity) pri korištenju CAT-a sa testovima širokog raspona skale (with large scale or high stakes tests?!) (Mills and Stocking, 1995; Stocking 1994; Green, Bock, Humphreys, and Reckase, 1984; FairTest, 1998). U ovom odlomku, dajem pregled slijedećih pitanja:

• Balansiranje sadržaja (Balancing content)
• Primjena čestica koje pripadaju skupu (Administering items belong to sets)
• Razmatranja u vezi s ispitanicima (Examinee Considerations)
• Item exposure
• Item pool characteristics
• Item pool size
• Shifting parameter estimates
• Stopping rules

Balansiranje sadržaja – Većina CAT-ova nastoji brzo pružiti jednu skupnu procjenu ispitanikove sposobnosti. Kako onda CAT može osigurati uravnoteženost sadržaja?

Proces izbora čestice korišten u ovom priručniku ovisi jedino o informativnosti čestice za izbor slijedeće čestice koja će biti primijenjena. Iako ova procedura može biti optimalna za određivanje ispitanikove opće razine sposobnosti, ona ne osigurava uravnoteženost sadržaja i ne garantira da možemo dobiti rezultate subtestova. Često želimo uravnotežiti sadržaj testova. Specifikacije testa za matematički test izračunavanja, na primjer, mogu zahtijevati da se određeni postotak čestica izvede zbrajanjem, oduzimanjem, množenjem i dijeljenjem.

Ako želimo dobiti upravo rezultate subtestova, onda se svaki subtest može tretirati kao nezavisna mjera i čestice unutar mjere se mogu adaptivno administrirati. Kada postoje visoke korelacije među subtestovima, procjene sposobnosti dobivene subtestom mogu se učinkovito koristiti kod započinjanja adaptivnog procesa za naredne subtestove.

Kingsbury i Zara (1989, 1991) opisuju uvjetno (ograničeno, "constrained") kompjuterski adaptivno testiranje (C-CAT) koje omogućava uravnoteženje sadržaja:

1. Privremena razina postignuća ispitanika se izračunava nakon primjene čestice.
2. Izračunava se postotak čestica koje su već primijenjene u svakom "subgoal"-u trenutnog testa.
3. Empirijski postoci se uspoređuju sa prethodno propisanim željenim postocima, te se identificira subgoal sa najvećom diskrepancijom (najmanje usklađen).
4. Sa subgoal-om koji ima najveće neslaganje, izabire se i daje ispitaniku čestica koja pruža najviše informacija na trenutnoj procjeni ispitanikove razine postignuća.

{4.With the subgoal with the largest discrepancy, the item providing the most information at the examinee's momentary achievement level estimate is selected and administered to the examinee.}

Veliki nedostatak ovog pristupa je u tome što grupe čestica moraju biti međusobno isključive. Kada broj nama važnih osobina čestica postane velik, broj čestica po particiji (potpodjeli) postaje malen. Nadalje, ne mora uvijek biti poželjno grupirati čestice u međusobno isključive podskupine.

Wainer i Kiely (1987) predložili su korištenje podtestova ("testlets") kao temelja za prilagođeno grananje. Čestice se grupiraju u male podtestove razvijene u skladu sa željenim specifikacijama testa. Ispitanik odgovara na sve čestice unutar podtestova. Rezultati na podtestu i prethodno primijenjenim podtestovima se zatim koriste za određivanje slijedećeg podtesta. Wainer, Kaplan i Lewis (1992) su pokazali da kada su veličine podtestova male, koristi od pravljenja i samih podtestova adaptivnima su skromne.

Swanson i Stocking (1993) i Stocking i Swanson (1993) opisuju model ponderiranih devijacija (WDM - weighted deviations model) koji izabire čestice koristeći linearno programiranje na osnovu brojnih simultanih uvjeta među kojima su statistički i sadržajni aspekti. Jedan uvjet bi bio da se maksimalizira informativnost čestice. Drugi uvjet bi mogle biti matematičke reprezentacije specifikacija testa ili model koji kontrolira da li se čestice preklapaju. Tradicionalni linearni model programiranja nije uvijek primjenjiv s obzirom da "neki uvjeti ne mogu biti zadovoljeni istovremeno sa nekim drugim (često međusobno ne-isključivim) uvjetom. WDM razrješava problem tretirajući uvjete kao poželjne osobine i prebacujući ih u objektivnu funkciju (ciljnu?; "moving them to the objective function") (Stocking and Swanson, 1993, p280).

Iako se WDM često može riješiti korištenjem tehnika linearnog programiranja, Swanson i Stocking (1993) nude heuristik za rješavanje WDMa:

• Za svaku česticu koja još nije primijenjena, izračunaj devijaciju za svaki od uvjeta kad bi čestica bila dodana u test.
• Sumiraj ponderirane devijacije za sve uvjete.
• Izaberi česticu sa najmanjom ponderiranom sumom devijacija.

Preferirani izbor bi ovisio o broju i prirodi željenih uvjeta

Primjena čestica koje pripadaju skupu – Može li se CAT prilagoditi česticama koje pripadaju skupinama?

U tipičnoj procjeni čitanja, ispitanik čita odlomak i odgovara na nekoliko pitanja u vezi tog odlomka. Podražajni materijal se prezentira samo jednom. U tom slučaju ne želimo kompjuterski adaptivan test koji tretira svaku česticu odvojeno. Na taj način ispitaniku bi isti podražaj mogao biti prikazan više puta, i on bi morao taj cijeli odlomak ponavljano čitati da bi odgovorio samo na jedno pitanje odjednom.

Svaki odlomak bi se moglo tretirati kao podtest na način kako je ranije opisano. Alternativni pristup, opisan od Millsa i Stockinga (1996) bio bi da se prikažu čestice unutar odlomka koje su najviše ciljane (najbliže trenutno procijenjenoj razini sposobnosti; op.prev.). Ovisno o specifikacijama testa, ispitanik bi mogao dobiti 3 od 10 pitanja vezanih uz određeni odlomak.

Pitanja vezana uz ispitanike – Koja su pitanja vezana uz ispitanike s obzirom na CAT?

Wise (1997) je postavio nekoliko pitanja iz perspektive ispitanika, uključujući preispitivanje odgovora na čestice i nepristranost. Primijetio je da istraživanja dosljedno pokazuju da ispitanici žele mogućnost da pregledaju svoje odgovore. Također je primijetio da kada ispitanici mijenjaju svoje odgovore, veća je vjerojatnost da će legitimno poboljšati svoje rezultate. Većina CAT-ova ne može udovoljiti želji ispitanika da pregledaju svoje odgovore (Wainerov (1987) "testlet" pristup je istaknuta iznimka). Kada bi pregled i promjena odgovora bili mogući, domišljat ispitanik bi mogao namjerno pogriješiti na početnim pitanjima. CAT program bi zatim pretpostavio nisku sposobnost ispitanika i izabrao seriju lakih pitanja. Domišljati ispitanik bi se zatim vratio i promijenio odgovore tako da budu točni. Rezultat bi mogao biti visok postotak točnih odgovora što bi rezultiralo umjetno visokom procjenom ispitanikove sposobnosti.

Iako siromašna i manjinska djeca imaju manji pristup računalima, Wise uočava da istraživanja o nepristranosti i CAT-u nemaju suglasne rezultate. Opazio je da postoje rasne i etničke razlike u korištenju i željenom trajanju testiranja. Štoviše, neka istraživanja su našla da Crnci bolje prolaze na kompjuterskim testovima nego na konvencionalnima. S obzirom da su nalazi bez zaključka Wise je zaključio da bi pitanje trebalo istražiti uzimajući u obzir svaki test koji se razvija.

Izloženost čestici – Kako se CAT može modificirati kako bi se osiguralo da se određene čestice ne koriste previše.

Bez dodatnih uvjeta, proces izbora čestice će izabrati statistički najbolje čestice. To će rezultirati time da će neke čestice imati veću vjerojatnost da će biti prezentirane od drugih, pogotovo u početku adaptivnog procesa. S druge strane u interesu nam je da se neke čestice ne koriste prečesto. Zaobilaženje procesa izbora čestice kako bi se ograničilo izlaganje čestice će bolje osigurati dostupnost informacije o razini čestice ("Overriding the item selection process to limit exposure will better assure the availability of item level information") i povećati sigurnost testa. Međutim, to ujedno umanjuje kvalitetu adaptivnog testa. Stoga, bio bi potreban dulji test.

Jedna način da kontroliramo izloženost je da po slučaju izaberemo česticu koja će biti primijenjena iz male skupine od čestica koje se najbolje uklapaju. Na primjer, McBride i Martin (1983) su predložili izabiranje po slučaju prve čestice od pet onih koje se najbolje uklapaju, druge iz četiri najbolje, treće iz grupe od tri i četvrte iz grupe od dvije. Peta i sve slijedeće čestice bile bi optimalno izabrane. Nakon početnih čestica, ispitanici bi bili dostatno diferencirani i optimalno bi dobili različite čestice. Kingsbury i Zara (1989, p 369) izvještavaju o dodatku opcije Zara-ovom CAT softveru da se po slučaju bira između dvije do deset najboljih čestica.

Sympson i Hetter (1985) razvili su pristup koji kontrolira izloženost čestice korištenjem modela vjerojatnosti. Pristup nastoji osigurati da vjerojatnost primjene, P(A) bude manja od neke vrijednosti r - očekivane, ali ne opažene, maksimalne mjere korištenja čestice. Ako P(S) označava vjerojatnost da je izabrana čestica optimalna, a P(A|S) označava vjerojatnost da je čestica primijenjena uz uvjet da je izabrana kao optimalna, onda P(A)=P(A|S)*P(S). Vrijednosti za P(A|S), parametri kontrole izloženosti za svaku česticu, mogu se odrediti simulacijskim studijama.

Karakteristike čestica ("Item pool characteristics ") – Može li se bilo koji test koristiti za CAT?

Lord (1980, p 152) je istaknuo da čestica pruža najviše informacija na b_i i da je najveća količina informacija koja može biti pružena:

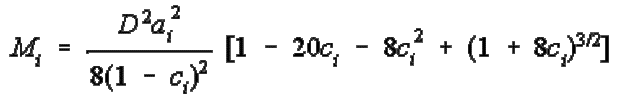
Maksimum informacija je funkcija parametara a_i i c_i. Čestica čija je a_i=1.00 biti će četiri puta efikasnija od čestice čija a_i=0.25. Čestica čija c_i=0.00 (tj. čestica na koju se odgovori po slučaju) biti će 1.6 puta efikasnija od čestice sa c_i= .25. (An item whose c_i=0.00 (i.e. a free response item) will be 1.6 times as effective and [trebalo bi pisati "as"] an item with c_i= .25.

Dakle, idealna skupina čestica za kompjuterski adaptivni test bila bi ona koja ima velik broj visoko diskriminativnih čestica na svakoj razini sposobnosti. Informacijske funkcije za te čestice izgledale bi kao niz zašiljenih distribucija na svim razinama theta-e.

Skupina čestica korištena u ovom priručniku nije idealna za kompjutersko adaptivno testiranje. Velik je broj nisko diskriminativnih čestica i težine čestica su većinom između -1.0 i 1.0.

Drugi način gledanja na banku čestica je gledanje sume informacijskih funkcija čestica. Informacijska funkcija ovoga testa pokazuje maksimalnu količinu informacija koje banka čestica može pružiti na svakoj pojedinoj razinibilo tradicionalnom ili CAT primjenom. Informacijska funkcija testa za skup čestica korišten u ovom testu je prikazan na slijedećoj slici:

.

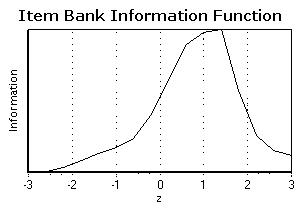
Informacija koju može pružiti ova banka čestica ima vrhunac za = 1.4. Banka čestica je najjača kada 0 < < 2. Ponavljam, ove krivulje definiraju gornje granice. U praksi, količina informacije biti će manja na svim razinama jer ispitanik odgovara samo na dio čestica iz banke čestica. U terminima CAT-a, manje čestica će biti potrebno primijeniti ispitanicima u rasponu 0 < < 2 kako bi se postigla određena razina precinzosti.

Veličina skupa čestica – Koliko velika ta skupina treba biti?

Potrebna veličina skupa čestica ovisi o namjeravanoj svrsi i karakteristikama testova koji se konstruiraju. Weiss (1985) ističe da su zadovoljavajuće primjene CAT-a postignute sa bankom čestica od 100 visoko kvalitetnih, dobro distribuiranih čestica. Također ističe da se preferiraju pravilno konstruirane skupine sa 150-200 čestica. Ako želimo uključiti realistični skup uvjeta (npr., slučajni izbor između najinformativnijih kako bi se smanjilo izlaganje uvijek istih čestica; izbor između nižih ili sastavnih vještina {"subskills"} kako bi se osigurala uravnoteženost sadržaja) ili primijeniti izbor sa vrlo visokim kriterijima ("very high stakes examination"L), onda će biti potrebna mnogo veća banka čestica/pitanja.

Pomicanje procjena parametara - Možemo li očekivati da će čestični parametri "item response" teorije biti stabilni pod kompjuterski adaptiranom primjenom čestica?

Brojne studije sa pravim ispitanicima dokumentirale su jednakost testova tipa papir olovka sa kompjuterski adaptivnim testovima pokazujući jednake procjene sposobnosti, jednake varijance i visoke korelacije (pogledajte Bergstrom, 1992 za sintezu 20 takvih studija). Ta identičnost implicira da su pretpostavke za CAT zadovoljene i da je CAT čvrst.

Dvije ključne pretpostavke na IRT utemeljenom kompjuterski adaptivnog testiranja su jednodimenzionalne banke čestica i fiksni parametri čestica. Dimenzionalnost banke čestica (ili populacije čestica - "item pool") ne bi trebala biti upitna s obzirom da se rutinski provjerava u sklopu razvoja kvalitetnog testa. Upitno je, međutim, da li se IRT parametri mijenjaju zbog načina primjene ili se možda mijenjaju tijekom vremena. Ispitujući sposobnosti osoba ("person-fit") papirnatim testom, Rudner, Bracey i Skaggs (1996) primijetili su da je sposobnost bila mnogo slabija za čestice na koje se odgovaralo uz pomoć kalkulatora negoli za iste čestice na koje se odgovaralo bez kalkulatora. Stoga, postoji vrlo realna mogućnost da parametri čestica kod CAT-a ne moraju biti isti kao kad se primjenjuju metodom papir-olovka. Također je bitna mogućnost da će se IRT parametri pomaknuti zbog promjena u nastavnom planu i programu ili u karakteristikama populacije. Pitanje pomaka parametara, međutim, moglo bi se lako razriješiti ponovnim izračunima IRT parametara nakon primjene CAT-a i usporedbe vrijednosti.

Pravila prekida – Kako odrediti kada prekinuti sa davanjem pitanja/čestica? Koje su implikacije različitih pravila prekida?

Jedna od teoretskih prednosti kompjuterskih adaptivnih testova je da se testiranje može nastaviti sve dok se ne postigne zadovoljavajuća razina preciznosti. Dakle, ako je populacija čestica (item pool) slaba na nekom odsječku kontinuuma sposobnosti, dodatne čestice se mogu primijeniti kako bi se smanjila standardna pogreška za pojedinca. Stocking (1987) je, međutim, pokazao da takvo testiranje različite duljine može rezultirati pristranim procjenama sposobnosti, osobito ako je test kratak. Nadalje, profinjenosti pravila prekida temeljenih na preciznosti (i zbog toga različite duljine testova) bilo bi teško objasniti laicima.

This tutorial was developed using Active Server Pages, the scripting language of Microsoft's Windows NT Internet Information Server.

From: Rudner, Lawrence M. (1998). An On-line, Interactive, Computer Adaptive Testing Tutorial, http://ericae.net/scripts/cat